10th Class Mensuration Chapter Solutions

Chapter – 10 Mathematics Mensuration Exercise 10.1 Solutions

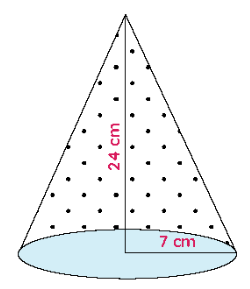
Question 1 : A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.

Solution:

Given: A right circular cone (joker’s cap) of base radius 7 cm and height 24 cm.

Since the cap is conical in shape, the area of the sheet required to make each cap will be equal to the curved surface area of the cone.

The curved surface area of a right circular cone of base radius(r) and slant height(l) is πrl

Slant height, l = √r² + h²  where h is the height of the cone.

Radius, r = 7 cm Height, h = 24 cm

Slant height,

l = √r² + h²

= √(7)² + (24)²

= √49 + 576

= √625

= 25 cm

Area of the sheet required to make each cap = πrl

= 22/7 × 7 cm × 25 cm

= 550 cm²

Area of the sheet required to make 10 such caps = 10 × 550 cm² = 5500 cm²

Answer = Thus, the area of the sheet required to make 10 such caps is 5500 cm².

Question 2 : A sports company was ordered to prepare 100 paper cylinders without caps for shuttle cocks. The required dimensions of the cylinder are 35 cm length / height and its radius is 7 cm. Find the required area of thin paper sheet needed to make 100 cylinders.

Solution :

Radius of the cylinder, r = 7 cm 

Height of the cylinder, h = 35 cm 

T.S.A. of the cylinder with lids at both ends = 2πr(r+h) 

= 2 × 22 7 22 7 × 7 × (7 + 35) 

= 2 × 22 7 22 7 × 7 × 42 = 1848 cm2.

Area of thin paper required for 100 cylinders = 100 × 1848 

= 184800 cm2 

= 184800 / 100 × 100 m2 

Answer = 18.48 m2 .

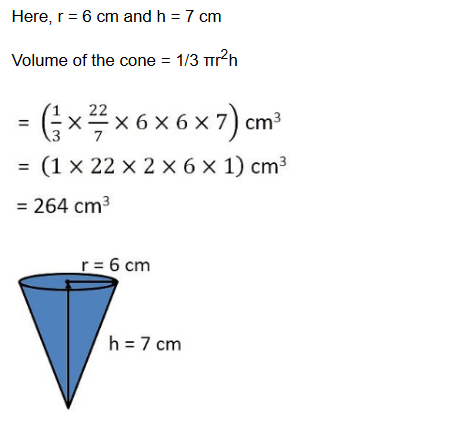
Question 3 : Find the volume of right circular cone with radius 6 cm and height 7 cm

Find the volume of the right circular cone with
i) radius 6 cm, height 7 cm  ii) radius 3.5 cm, height 12 cm

Solution:

Volume of a cone of base radius r, and height h, = 1/3πr²h

i) Radius of the cone, r = 6 cm

Height of the cone, h = 7 cm

Volume of the cone = 1/3πr²h

= 1/3 × 22/7 × 6 cm × 6 cm × 7 cm

Answer = 264 cm³

ii) Radius of the cone, r = 3.5 cm

Height of the cone, h = 12 cm

Volume of the cone = 1/3πr²h

= 1/3 × 22/7 × 3.5 cm × 3.5 cm × 12 cm

Answer = 154 cm³

Question 4 : The lateral surface of a cylinder is equal to the curved surface of a cone. If the radius will be the same. Find the ratio of the height of the cylinder and the slant height of the cone.

Solution : To solve the problem step by step, we will follow the given information and apply the relevant formulas.

The formulas for the lateral surface area (curved surface area) of a cylinder and a cone are:
– Curved Surface Area of Cylinder = 2πrh
– Curved Surface Area of Cone = πrl

According to the problem, we have:
2πrh=πrl

Since both sides of the equation have πr (where r is the radius), we can cancel πr from both sides (assuming r≠0):
2h=l

To find the ratio of the height of the cylinder (h) to the slant height of the cone (l), we can rearrange the equation:
h=l/2
Thus, the ratio of h to l is:
h/l=1/2

Answer = The ratio of the height of the cylinder to the slant height of the cone is:
1:2

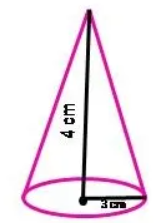
Question 5 : A self help group wants to manufacture joker’s caps (conical caps) of 3 cm radius and 4 cm height. If the available colour paper sheet is 1000 cm2, then how many caps can be manufactured from that paper sheet?

Solution :

Question 6 : A cylinder and cone have bases of equal radii and are of equal hieghts. Show that their volumes are in the ratio 3:1.

Solution :

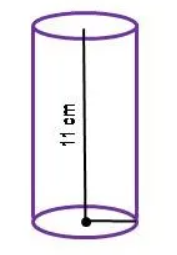
Question 7 : A solid iron rod has cylindrical shape. Its height is 11 cm. and base diameter is 7 cm. Then find the total volume of 50 rods?

Solution :

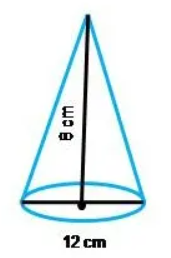
Question 8 : A heap of rice is in the form of a cone of diameter 12 m. and height 8 m. Find its volume? How much canvas cloth is required to cover the heap?

Solution :

Question 9 : The curved surface area of a cone is 4070 cm2 and its diameter is 70 cm. What is its slant height?

Solution :

Chapter – 10 Mathematics Mensuration Exercise 10.2 Solutions

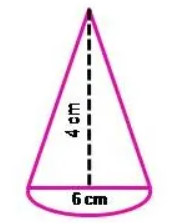
Question 1 : A toy is in the form of a cone mounted on a hemisphere of the same diameter. The Diameter of the base and the height of the cone are 6 cm and 4 cm respectively. Determine the surface area of the toy.

Solution :

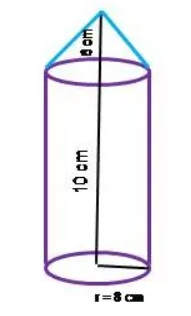
Question 2 : A solid is in the form of a right circular cylinder with a hemisphere at one end and a cone at the other end. The radius of the common base is 8 cm and the heights of the cylindrical and conical portions are 10 cm and 6 cm respectively. Find the total surface area of the solid.

Solution : Total surface area = C.S.A. of the cone + C.S.A. of cylinder + C.S.A of the hemisphere.

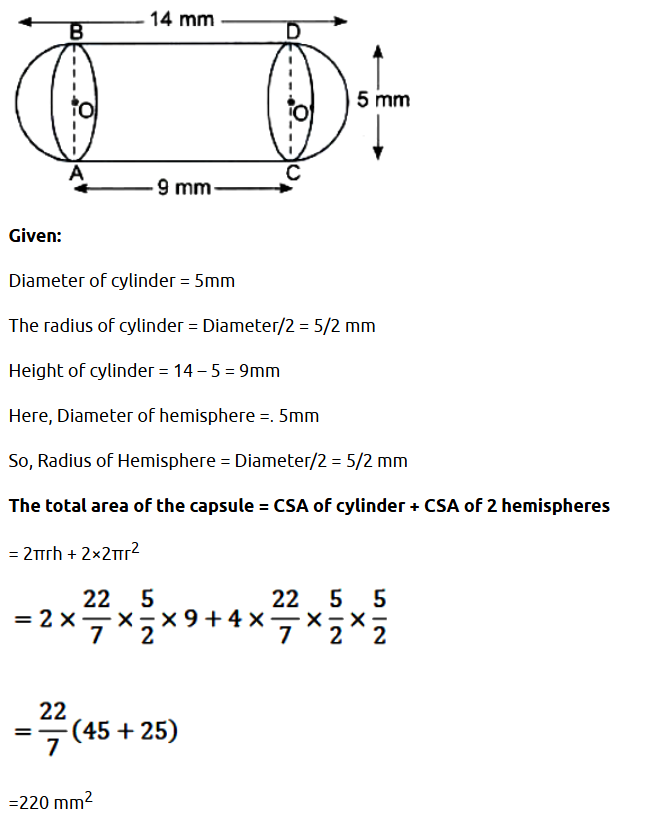
Question 2 : A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the entire capsule is 14 mm, and the diameter of the capsule is 5 mm. Find its surface area.

Solution :

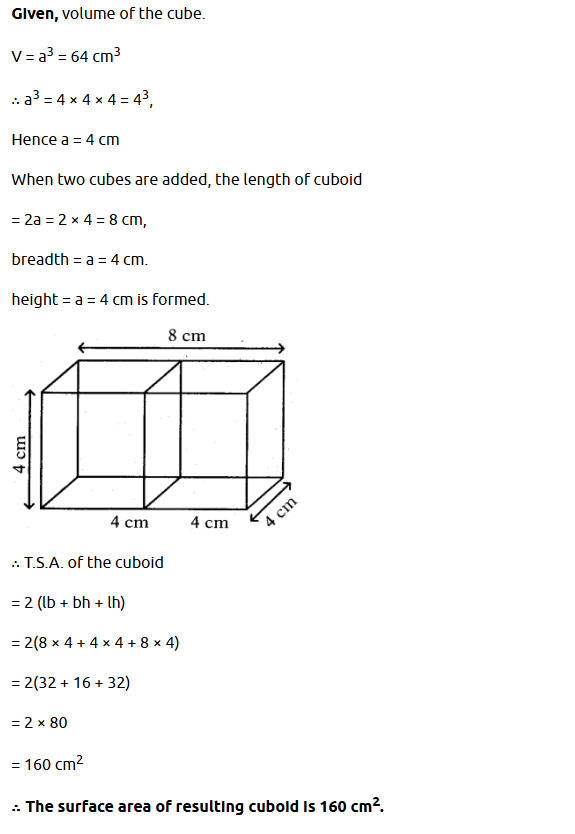
Question 4 : Two cubes each of volume 64 cm2 are joind end together. Find the surface area of the resulting cuboid.

Solution :

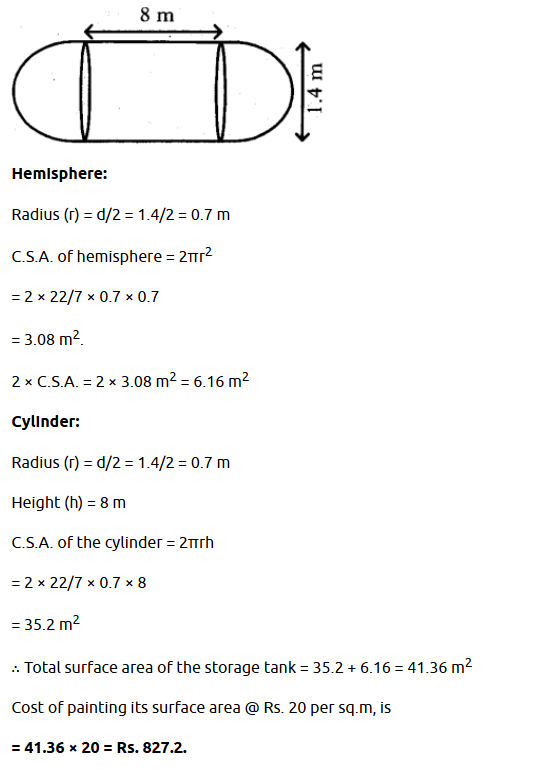
Question 5 : A storage tank consists of a circular cylinder with a hemisphere stuck on either end. If the external diameter of the cylinder be 1.4 m. and its length be 8 m. Find the cost of painting it on the outside at rate of Rs. 20 per m2.

Solution : Total surface area of the tank = 2 × C.S.A. of hemisphere + C.S.A. of cylinder.

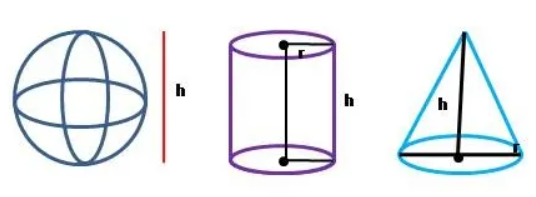
Question 6 : A sphere, a cylinder and a cone have the same radius and same height. Find the ratio of their volumes. Diameter of the sphere is equal to the height of the cylinder and the cone.

Solution :

Question 7 : A hemisphere is cut out fron one face of a cubical wooden block such that the diameter of the hemisphere is equal to the side of the cube. Determine the total surface area of the remaining solid.

Solution :

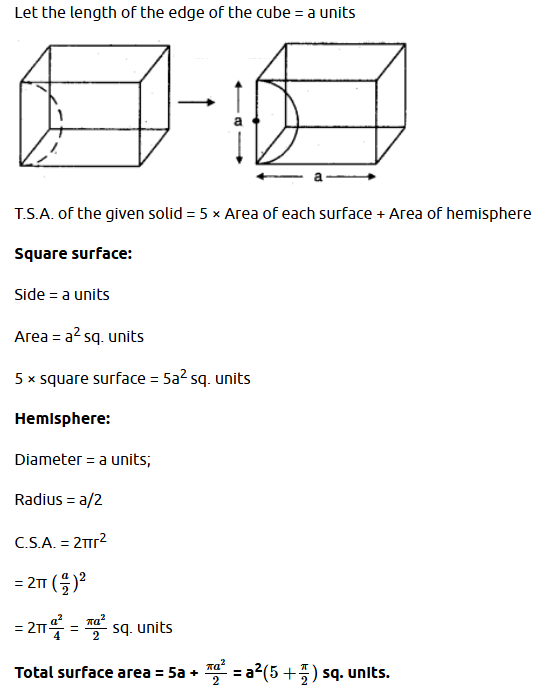
Question 8 : A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm. and its radius of the base is 3.5 cm. Find the total surface area of the article.

Solution :

a

Chapter – 10 Mathematics Mensuration Exercise 10.3 Solutions

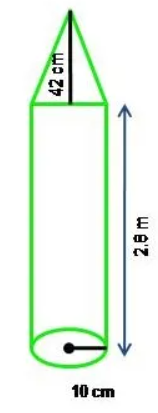
Question 1 : An iron pillar consists of a Cylindrical portion of 2.8 m. height and 20 cm. in diameter and a cone of 42 cm. height surmounting it. Find the weight of the pillar if 1 cm3 of iron weighs 7.5 g.

Solution : Volume of the iron pillar = Volume of the cylinder + Volume of the cone 

Cylinder:

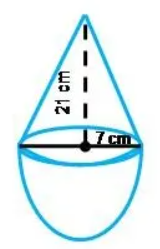
Question 2 : A toy is made in the form of hemisphere surmounted by a right cone whose circular base is joined with the plane surface of the hemisphere. The radius of the base of the cone is 7 cm. and its volume is 3/2 of the hemisphere. Calculate the height of the cone and the surface area of the toy correct to 2 places of decimal.

Solution :

Question 3 : Find the volume of right circular cone with radius 6 cm and height 7 cm.

Solution :

Question 4 : A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the hemisphere is immersed in the tub. If the radius of the hemi-sphere is 3.5 cm and height of the cone outside the hemisphere is 5 cm, find the volume of the water left into hr tub. (Take π = 22/7)

Solution :

Question 5 : In the adjacent figure, the height of a solid cylinder is 10 cm and diameter 7 cm. Two equal conical holes of radius 3 cm and height 4 cm are cut off as shown in the figure. Find the volume of the remaining solid.

Solution :

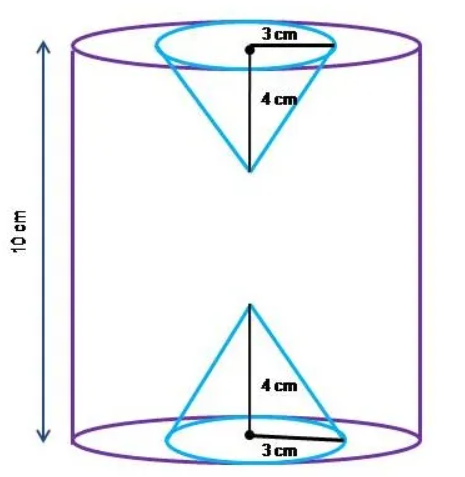
Question 6 : Spherical marbles of diameter 1.4 cm. are dropped into a cylindrical beaker of diameter 7 cm., which contains some water. Find the number of marbles that should be dropped into the beaker, so that water level rises by 5.6 cm.

Solution : Rise in the water level is seen in cylindrical shape of Radius = Beaker radius 

= d/2 = 7/2 = 3.5 cm

Question 7 : A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand.

Solution :